Relating Time Series in Data to Spatial Variation in the Reservoir Using Wavelets
Investigator: A. A. Awotunde, Petroleum Engineering
Accurate description of the reservoir is crucial to reservoir management. Yet, due to the complex nature of reservoir heterogeneity, obtaining accurate description of the reservoir poses a big challenge.
Two main challenges in reservoir description are: (1) obtaining accurate description of the reservoir heterogeneity; and (2) deploying computationally efficient and less memory-demanding algorithms to characterize the reservoir.
The difficulty in obtaining accurate reservoir description arises from the fact that information available in the form of observed data is usually insufficient to resolve the detailed information contained in the heterogeneous reservoir. This leads to non-uniqueness of the inverse solution thus making it possible to match observed dataset using different combinations, sometimes typically unrealistic combinations, of reservoir parameters. We illustrate this problem by solving an inverse problem to obtain the permeability distribution in the eight rings of a radial composite reservoir. The conventional least squares procedure to obtain the inverse solution uses the minimization algorithm in Equation (1).

In Equation (1), is the vector of model parameters, in this case, the reservoir permeability distribution. The vector containing all is the vector of observed data while the vector containing all is the vector of data computed from the forward model. This procedure gives a very good match to the observed data as shown in Figure 1. However, the reservoir parameters modeled by the procedure are different from the actual reservoir parameters as seen in Figure 2.
The second problem faced in reservoir description is the necessity to deal with a huge set of reservoir parameters and/or data. This arises, in part, because every location in the reservoir is unique and it will take an infinite number of reservoir parameters to obtain an exact characterization of the reservoir. This is impractical. The practice is to represent the reservoir by a finite number of grid blocks, with each block having a value of the reservoir parameter assigned to it. Even then, the number of grid cells may be very large requiring a large memory space as well as making the inverse problem very slow. In addition, the advent of permanent downhole gauges has made measured dataset become large and the use of such huge data in inverse problem analysis may be prohibitively expensive.
The focal point of this research is to determine the minimal sets of model parameters and data required to accurately describe the reservoir. Recent research efforts have focused on the reparameterization of reservoir parameters with a small number of model parameters that can represent the original characterization without significant loss of accuracy. One of such efforts is the use of wavelet analysis to reparameterize the model space presented by Lu and Horne1. In this research we move a step further by using wavelets not only to re-parameterize the model space, but also to reduce the dimension of the data space. Thus, we solve the inverse problem in the wavelet domain.

Figure 1: Match to observed data in an 8-ring composite reservoir
Because high dimensional spaces are often highly redundant we use a small number of wavelet coefficients to characterize both the model space and the data space. Therefore, in our analysis, the minimization algorithm in Equation (1) is expressed as (2) where is a subset of the
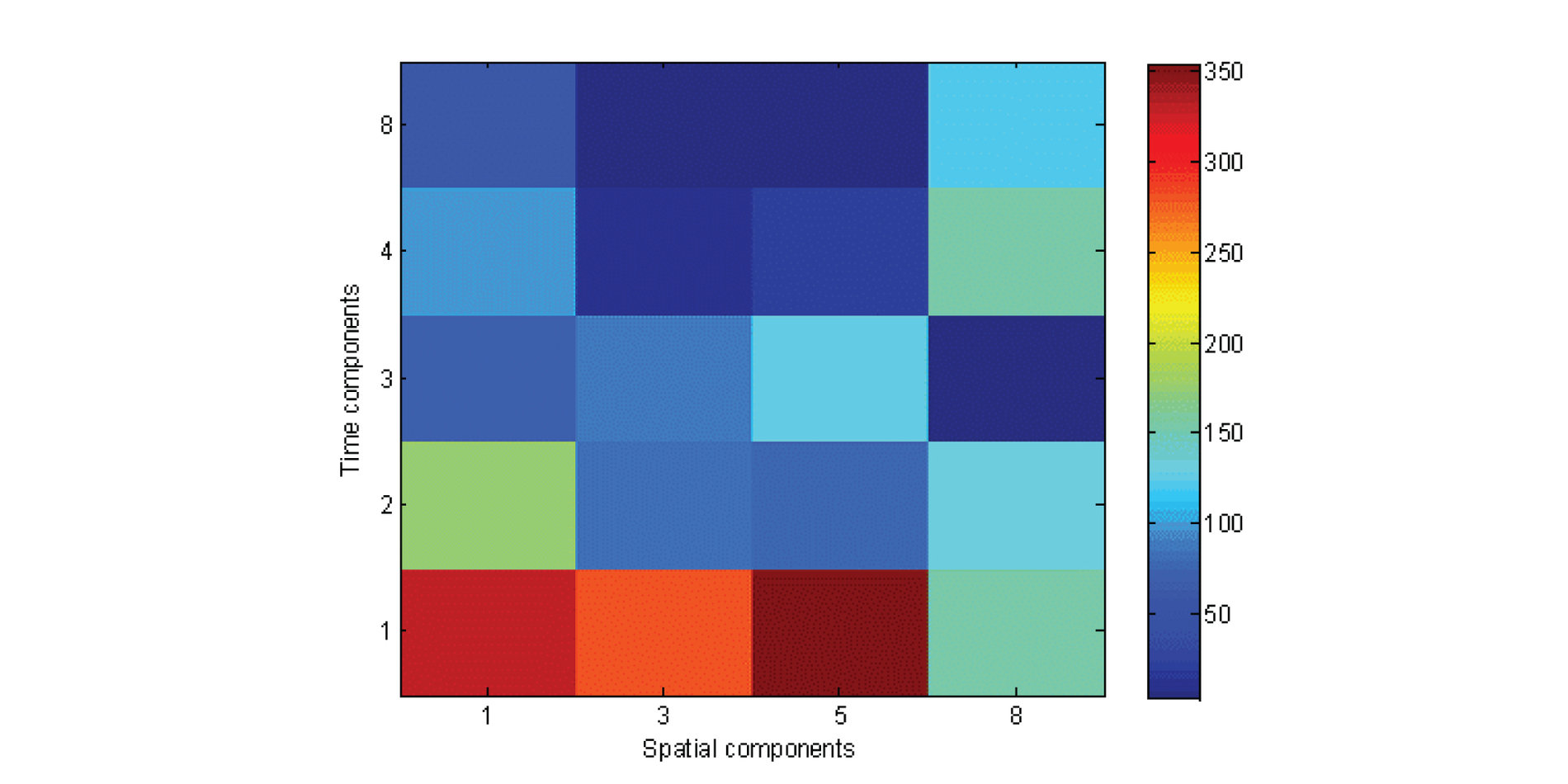
wavelet coefficients of the model parameters, is the subset of the wavelet transform of the observed data and is the subset of the wavelet transform of the calculated data. The coefficients are chosen based on the wavelet sensitivity matrix. Figure 3 shows a sample wavelet coefficient matrix of size

Figure 2: Permeability distributions modeled by conventional least-squares method
The blue regions of the wavelet sensitivity coefficient matrix in Figure 3 indicate
coefficients with very low absolute values. We observe that the 6th and 7th components of the spatial coefficients play an insignificant role in the modeling of the observations. The 2nd and 4th spatial coefficients are also less significant than the remaining coefficients. Most of the time components are in fact redundant. Eliminating coefficients based on preset thresholds leads to reduction in the dimensions of the model space, data space and wavelet sensitivity coefficient matrix. The reduced wavelet sensitivity matrix is displayed in Figure 4.
The procedure presented above is typically performed at all iterations of the least squares regression algorithm. As the iteration progresses, the time and spatial coefficients improve. This procedure stabilizes the algorithm and speeds up the regression process thus improving the quality of parameter estimation.
In Figure 5 we compare the permeability distributions obtained from this approach to those obtained from conventional procedure and from the work of Lu and Horne1. We observe that the algorithm given by Lu and Horne1 and that given in this work produced more accurate results than the conventional algorithm. In Figure 6 we also observe reduction in number of function evaluations when the regression is performed in the wavelet domain.
Another case considered is modeling the permeability distribution in a 32-ring radial composite reservoir. All the approaches used give very good match to the data (shown in Figure 7) yet the permeability distributions obtained from the various approach are different in the region close to the well bore as shown in Figure 8.

Figure 5: Permeability distributions in an 8-ring composite reservoir modeled from different procedures

Figure 7: Match of modeled data to observed data in an 8-ring composite reservoir
In summary the procedure presented involves the following:
- Transformation of the model and data spaces.
- Dimension reduction.
- Minimization of the object function using the reduced sets of model parameters/data. Further work in will consider the application of this approach to a fully distributed reservoir simulation studies.
References:
1. Lu, P. and Horne, R. N.: "A Multiresolution Approach to Reservoir Parameter Estimation Using Wavelet Analysis," paper SPE 62985 presented at the SPE Annual Technical conference and Exhibition, Dallas, 1-4 October, 2000.
2. Lu, P.: "Reservoir Parameter Estimation Using Wavelet Analysis," Ph.D. dissertation, Stanford University, Stanford, California, May 2001.
3. Sahni, I., and Horne, R.N.: "Generating Multiple History-Matched Reservoir-Model Realizations Using Wavelets," SPEREE (June 2006) 217.
4. Sahni, I.: “Multiresolution Reparameterization and Partitioning of Model Space for Reservoir Characterization,” Ph.D. dissertation, Stanford University, Stanford, California, August 2006.



